K-평균 군집화(K-Means Clustering) 개념과 구현
K-평균 군집화(K-Means Clustering)는 데이터를 K개의 그룹으로 나누는 군집화(Clustering) 알고리즘이다.
주어진 데이터에서 각 데이터 포인트를 가장 가까운 중심(centroid)으로 할당하고, 중심을 반복적으로 업데이트하여 최적의 군집을 찾는다.
K-평균 군집화는 비지도 학습(Unsupervised Learning) 방법에 속한다.
(군집화는 집단을 만드는 역할, 지도학습-분류는 집담에 데이터를 분류해 넣는 역할)
1. K-평균 군집화의 기본 개념
K-평균 군집화는 다음과 같은 단계를 반복하여 최적의 군집을 형성한다.
- 데이터에서 K개의 중심(centroid)을 무작위로 초기화한다.
- 각 데이터 포인트를 가장 가까운 중심에 할당하여 군집을 형성한다.
- 각 군집의 중심을 다시 계산하여 새로운 중심을 찾는다.
- 새로운 중심을 기준으로 다시 군집을 할당하고, 중심이 더 이상 변화하지 않을 때까지 이 과정을 반복한다.
K-평균 알고리즘은 사용자가 미리 K값을 정해야 한다는 단점이 있으며, 최적의 K값을 찾기 위해 엘보우(Elbow) 기법과 실루엣(Silhouette) 점수와 같은 방법을 사용할 수 있다.
- K=1이면 한 개의 이웃만 참고하여 예측하므로, 노이즈에 취약하고 과적합 가능성이 큼.
- 결정 경계가 너무 복잡해져 일반화 성능이 떨어질 수 있음.
✅ 일반적으로 K는 홀수(3, 5, 7)로 설정하는 것이 좋음.
- K가 너무 작으면(예: 1, 2) 과적합 위험 증가
- K가 너무 크면(예: 20, 30) 데이터가 너무 평균화되어 분류 성능이 저하될 수 있음.
2. K-평균 군집화의 특징
- 데이터가 사전에 라벨링되지 않은 경우에도 패턴을 발견하는 데 유용하다.
- 데이터가 구형(원형) 클러스터를 가질 때 효과적이며, 복잡한 형태의 클러스터에서는 성능이 저하될 수 있다.
- 초기 중심값의 설정에 따라 결과가 달라질 수 있으므로, 여러 번 실행하여 최적의 군집을 찾는 것이 중요하다.
3. K-평균 군집화의 장점과 단점
장점
- 계산 속도가 빠르고 대규모 데이터에서도 비교적 효율적이다.
- 해석이 용이하며 직관적인 알고리즘이다.
- 특정 분야(이미지 분할, 고객 세분화 등)에서 널리 사용된다.
이미지 분할(Image Segmentation)과 압축에서 K-Means 활용
- K-Means는 손실 압축(Lossy Compression) 기법에서 자주 사용됨.
- 비슷한 색상 픽셀을 같은 군집(Cluster)으로 묶어 색상 수를 줄여 데이터 크기를 감소시킴.
단점
- K값을 미리 설정해야 하며, 잘못된 K값 선택은 성능 저하를 초래할 수 있다.
- 원형 군집이 아닌 경우(예: 타원형 또는 비선형 구조) 성능이 낮을 수 있다.
- 이상치(Outlier)에 민감하여 중심값이 왜곡될 가능성이 있다.
4. K-평균 군집화 구현 (Python 예제)
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성
np.random.seed(42)
X = np.vstack([
np.random.normal(loc=[2, 2], scale=0.5, size=(50, 2)),
np.random.normal(loc=[8, 8], scale=0.5, size=(50, 2)),
np.random.normal(loc=[5, 14], scale=0.5, size=(50, 2))
])
# K-평균 군집화 수행
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
# 결과 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', marker='o', edgecolors='k')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, label='Centroids')
plt.legend()
plt.title("K-Means Clustering")
plt.show()
이 코드는 무작위로 생성한 데이터를 세 개의 군집으로 나누고, 결과를 시각화하는 예제이다.

5. K-평균 군집화의 활용 예제
예제 1: 고객 세분화
온라인 쇼핑몰에서 고객 데이터를 분석하여 비슷한 소비 패턴을 가진 고객들을 그룹화할 수 있다. 고객의 연간 구매 금액, 구매 빈도, 방문 횟수 등의 데이터를 기반으로 K-평균 군집화를 수행하면, VIP 고객, 일반 고객, 신규 고객 등의 그룹을 나눌 수 있다. 이를 통해 맞춤형 마케팅 전략을 수립할 수 있다.
from sklearn.preprocessing import StandardScaler
import pandas as pd
# 샘플 고객 데이터 생성
data = {
"Annual_Income": [15, 16, 17, 50, 52, 53, 100, 105, 110],
"Spending_Score": [39, 40, 45, 60, 65, 70, 15, 18, 20]
}
df = pd.DataFrame(data)
# 데이터 정규화
scaler = StandardScaler()
scaled_data = scaler.fit_transform(df)
# K-평균 군집화 수행
kmeans = KMeans(n_clusters=3, random_state=42)
df["Cluster"] = kmeans.fit_predict(scaled_data)
print(df)
이 코드는 고객 데이터를 K-평균 군집화하여 소비 패턴에 따라 그룹을 나누는 예제이다.
예제 2: 이미지 색상 압축
이미지의 색상을 줄이는 데 K-평균 군집화를 사용할 수 있다. 예를 들어, 고해상도 이미지에서 1,000만 개의 색상을 단 16개의 색상으로 줄이면, 압축된 이미지를 생성할 수 있다.
from sklearn.cluster import KMeans
from skimage import io
import numpy as np
# 이미지 로드
image = io.imread("sample.jpg")
pixels = image.reshape(-1, 3)
# K-평균 군집화 적용
kmeans = KMeans(n_clusters=16, random_state=42)
kmeans.fit(pixels)
compressed_pixels = kmeans.cluster_centers_[kmeans.labels_]
compressed_image = compressed_pixels.reshape(image.shape)
# 압축된 이미지 시각화
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(image)
plt.title("Original Image")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(compressed_image.astype(np.uint8))
plt.title("Compressed Image (16 Colors)")
plt.axis("off")
plt.show()
이 코드는 K-평균 군집화를 사용하여 원본 이미지의 색상을 16개의 주요 색상으로 줄이는 예제이다.

K-Means를 활용한 이미지 압축 과정
- 이미지를 픽셀 데이터(RGB 값)로 변환
- K개의 색상 중심(centroid) 생성 후, 각 픽셀을 가장 가까운 중심으로 할당
- 군집별 대표 색상을 사용하여 새로운 이미지 생성
- 색상 수를 줄임으로써 압축된 이미지 완성
예제 3: 이상치 탐지
K-평균 군집화를 사용하여 정상적인 데이터 포인트와 이상치를 구별할 수 있다. 예를 들어, 은행 거래 데이터를 분석하여 비정상적인 거래(사기)를 탐지하는 데 활용할 수 있다.
import numpy as np
# 샘플 거래 데이터 생성
transactions = np.array([
[50, 1], [60, 1], [55, 2], [700, 5], [58, 2], [62, 1], [750, 5], [65, 2]
])
# K-평균 군집화 적용
kmeans = KMeans(n_clusters=2, random_state=42)
labels = kmeans.fit_predict(transactions)
# 이상치 탐지
outliers = transactions[labels == labels.max()]
print("Detected Outliers:", outliers)
최적의 K값을 찾는 방법: 엘보우 기법과 실루엣 점수
K-평균(K-Means) 알고리즘은 군집의 개수(K)를 사용자가 미리 설정해야 한다는 단점이 있다. 따라서 최적의 K값을 찾기 위해 엘보우(Elbow) 기법과 실루엣(Silhouette) 점수를 활용할 수 있다.
주로 엘보우 기법이 사용됨.
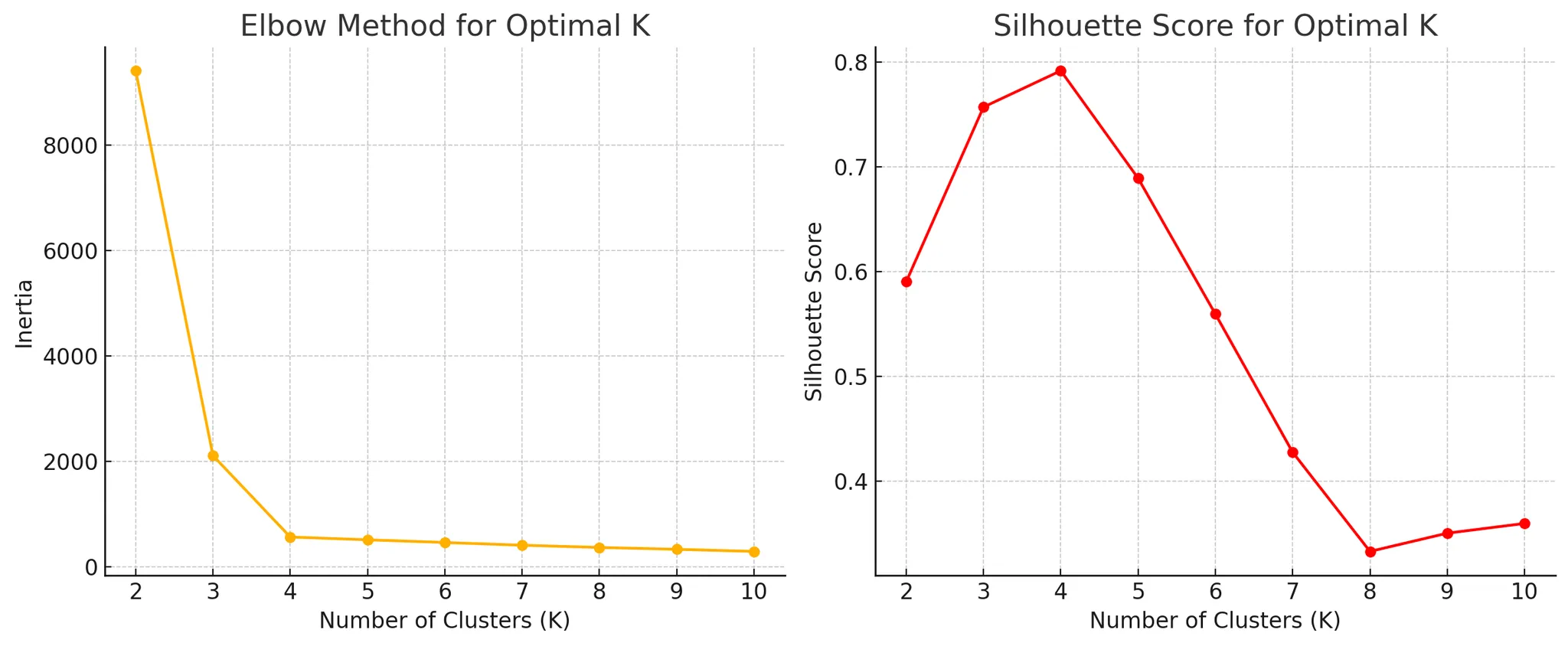
- 엘보우 기법(Elbow Method): K값에 따른 군집 내 변동 값(Inertia)을 계산하여, 그래프의 기울기가 급격히 완만해지는 지점(엘보우 포인트)을 최적의 K값으로 선택한다.
- 실루엣 점수(Silhouette Score): 각 데이터 포인트가 자신의 군집과 얼마나 밀접하게 묶여 있으며, 다른 군집과는 얼마나 분리되어 있는지를 평가하는 지표이다. 실루엣 점수가 높을수록 군집화가 잘 되어 있음을 의미한다.
1. 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.datasets import make_blobs
# 샘플 데이터 생성
np.random.seed(42)
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=1.0, random_state=42)
2. 엘보우 기법을 이용한 최적 K값 찾기
# K 값별 관성(Inertia) 저장
inertia = []
k_range = range(1, 11)
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
inertia.append(kmeans.inertia_)
# 엘보우 차트 그리기
plt.figure(figsize=(8, 5))
plt.plot(k_range, inertia, marker='o')
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Inertia")
plt.title("Elbow Method for Optimal K")
plt.xticks(k_range)
plt.show()
이 코드를 실행하면 엘보우 차트가 생성되며, 곡선이 급격히 꺾이는 지점이 최적의 K값이 된다.

3. 실루엣 점수를 이용한 최적 K값 찾기
# K 값별 실루엣 점수 저장
silhouette_scores = []
for k in range(2, 11): # 실루엣 점수는 최소 2개 이상의 클러스터가 필요
kmeans = KMeans(n_clusters=k, random_state=42)
labels = kmeans.fit_predict(X)
silhouette_scores.append(silhouette_score(X, labels))
# 실루엣 점수 그래프 그리기
plt.figure(figsize=(8, 5))
plt.plot(range(2, 11), silhouette_scores, marker='o', color='red')
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Silhouette Score")
plt.title("Silhouette Score for Optimal K")
plt.xticks(range(2, 11))
plt.show()
이 코드를 실행하면 실루엣 점수 차트가 생성되며, 점수가 가장 높은 K값이 최적의 클러스터 개수가 된다.
4. 결론
- 엘보우 기법을 통해 K값이 4에서 급격히 기울기가 완만해지는 것을 확인할 수 있다.
- 실루엣 점수를 보면, 가장 높은 점수를 갖는 K값이 최적의 군집 개수로 판단할 수 있다.
'STUDY' 카테고리의 다른 글
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 27-1 인공신경망 ANN (1) | 2025.03.14 |
|---|---|
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 26 kNN, SVM, 로지스틱 회귀 실습 (0) | 2025.03.13 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 24 로지스틱 회귀, 실습 (1) | 2025.03.11 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 23 선형 회귀분석 복습, 실습 (2) | 2025.03.10 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day22 머신러닝 기초, 로지스틱 회귀 실습 (0) | 2025.03.07 |



