1. 로지스틱 회귀 개념
- 로지스틱 회귀는 이진 분류(Binary Classification) 문제를 해결하는 지도 학습(Supervised Learning) 알고리즘이다.
- 선형 회귀와 달리 종속 변수( )가 연속형이 아닌 이진 값(0 또는 1)을 가지는 경우 사용된다.
- 예측값을 0~1 사이의 확률 값으로 변환하기 위해 시그모이드 함수(Sigmoid Function)를 적용한다.
1.1 시그모이드 함수(Sigmoid Function)

- $z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n$ (선형 결합)
- $h(x)$ 값은 항상 0과 1 사이의 확률 값을 가진다.
- 특정 임계값(보통 0.5) 기준으로 0과 1을 구분한다.
- h(x) >=0.5$ 이면 클래스 1
- h(x) < 0.5$ 이면 클래스 0
- 시그모이드 함수는로그 스케일을 가지며, 로지스틱 함수(Logistic function)라고도 불린다.
- 로지스틱 회귀(Logistic Regression)는 시그모이드 함수를 이용하여 입력 z를 이진값으로 변환하는 회귀 모델이다.
- 여기서 z = wx + b 형태로 선형 회귀식이 들어감.
2. 로지스틱 회귀 활용 사례
| 활용 분야 | 설명 |
| 이메일 스팸 필터링 | 이메일이 스팸(1)인지 정상 메일(0)인지 분류 |
| 고객 이탈 예측 | 고객이 이탈할 가능성(1)인지 유지될 가능성(0)인지 예측 |
| 질병 진단 | 환자가 특정 질병에 걸릴 가능성이 있는지(1: 있음, 0: 없음) 예측 |
| 대출 승인 | 대출 신청자가 대출을 갚을 가능성이 있는지(1) 또는 불가능한지(0) 예측 |
3. 로지스틱 회귀 모델 학습 및 평가
3.1 로지스틱 회귀 모델 학습 (Python 코드 예제)
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
# 데이터 로드
df = pd.read_csv("customer_churn.csv")
# 독립 변수(X)와 종속 변수(y) 설정
X = df.drop(columns=["Churn"])
y = df["Churn"]
# 학습/테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 로지스틱 회귀 모델 학습
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측 및 평가
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"정확도: {accuracy:.2f}")
print("분류 보고서:\\n", classification_report(y_test, y_pred))
- 로지스틱 회귀 코드 주석
import pandas as pd # 데이터 분석 및 처리 라이브러리
from sklearn.model_selection import train_test_split # 데이터를 학습/테스트 세트로 분할하는 모듈
from sklearn.linear_model import LogisticRegression # 로지스틱 회귀(이진 분류) 모델
from sklearn.metrics import accuracy_score, classification_report # 모델 평가(정확도, 성능 보고서)
# 📌 1. 데이터 로드
df = pd.read_csv("customer_churn.csv") # 고객 이탈(Churn) 데이터 불러오기
# 📌 2. 독립 변수(X)와 종속 변수(y) 설정
X = df.drop(columns=["Churn"]) # "Churn" 열을 제외한 나머지 데이터를 독립 변수(특징)로 설정
y = df["Churn"] # "Churn" 열을 종속 변수(목표 변수)로 설정 (0: 유지, 1: 이탈)
# 📌 3. 학습 데이터와 테스트 데이터로 분리 (80% 학습, 20% 테스트)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 📌 4. 로지스틱 회귀 모델 학습
model = LogisticRegression() # 로지스틱 회귀 모델 객체 생성
model.fit(X_train, y_train) # 학습 데이터(X_train, y_train)로 모델 학습
# 📌 5. 예측 및 평가
y_pred = model.predict(X_test) # 테스트 데이터(X_test)로 예측 수행
accuracy = accuracy_score(y_test, y_pred) # 실제값(y_test)과 예측값(y_pred) 비교하여 정확도 계산
# 📌 6. 결과 출력
print(f"정확도: {accuracy:.2f}") # 모델의 정확도 출력
print("분류 보고서:\\n", classification_report(y_test, y_pred)) # Precision, Recall, F1-score 등 분류 성능 보고서 출력
- 데이터 로드: pd.read_csv()로 데이터를 불러옴
- 독립 변수(X)와 종속 변수(y) 설정:
- X: Churn을 제외한 나머지 특징(Feature)들
- y: Churn 열 (목표 변수, 고객 이탈 여부)
- 데이터 분할: train_test_split()을 사용해 80% 학습, 20% 테스트 데이터로 분리
- 모델 학습: LogisticRegression().fit()을 사용해 학습 데이터로 모델 훈련
- 예측 수행: model.predict()를 사용해 테스트 데이터로 예측
- 모델 평가:
- accuracy_score() → 정확도 계산
- classification_report() → Precision, Recall, F1-score 등 성능 지표 출력
4. 분류 모델 평가 지표
TP, TN, FP, FN은 이진 분류(Binary Classification) 모델에서 예측 결과를 평가하는 개념.
4.1 혼동 행렬(Confusion Matrix)
- TP, TN, FP, FN 개념을 정리한 표 형태
- 모델의 예측 오류를 분석하는 데 사용됨
| 예측 / 실제 | 실제 0 (음성) | 실제 1 (양성) |
| 예측 0 (미전환) | TN (진음성) | FN (위음성) |
| 예측 1 (전환) | FP (위양성) | TP (진양성) |
- TP (True Positive, 진짜 양성) → 실제 1(이탈)이고, 모델도 1(이탈)로 예측
- TN (True Negative, 진짜 음성) → 실제 0(유지)이고, 모델도 0(유지)로 예측
- FP (False Positive, 거짓 양성) → 실제 0(유지)인데 모델이 1(이탈)로 예측 (잘못 예측)
- FN (False Negative, 거짓 음성) → 실제 1(이탈)인데 모델이 0(유지)로 예측 (잘못 예측)
4.2 주요 성능 지표
1.정확도 (Accuracy)
- 전체 데이터 중 맞춘 비율
- 데이터 불균형이 심하면 신뢰하기 어려움

2. 정밀도 (Precision)
- 모델이 1(이탈)로 예측한 것 중 실제로 맞춘 비율
- FP(잘못된 긍정 예측)를 줄이는 데 중요
- 예시: 스팸 필터, 광고 타겟팅

3. 재현율 (Recall)
- 실제 1(이탈) 중에서 모델이 맞춘 비율
- FN(실제 1인데 모델이 0으로 예측한 것)을 줄이는 데 중요
- 예시: 암 진단, 금융 사기 탐지

4. F1-score
- Precision과 Recall의 균형을 고려한 지표(조화평균)
- Precision이 높아도 Recall이 낮으면 안 좋음 → 둘의 균형이 필요
- F1-score가 높을수록 균형 잡힌 좋은 모델
- 데이터가 불균형할 때 유용

5. 분류 보고서 해석 (classification_report() 결과 분석)
print(classification_report(y_test, y_pred))
출력 예시:
precision recall f1-score support
0 0.85 0.90 0.87 400
1 0.75 0.65 0.70 200
accuracy 0.82 600
macro avg 0.80 0.78 0.79 600
weighted avg 0.81 0.82 0.81 600
5.1 개별 지표 해석
- Precision (정밀도)
- 0 (유지): 0.85 → "유지로 예측한 것 중 85%가 실제 유지 고객"
- 1 (이탈): 0.75 → "이탈로 예측한 것 중 75%가 실제 이탈 고객"
- Recall (재현율)
- 0 (유지): 0.90 → "실제 유지 고객 중 90%를 유지로 맞췄다."
- 1 (이탈): 0.65 → "실제 이탈 고객 중 65%만 이탈로 예측했다." (35%는 놓침)
- F1-score
- 0 (유지): 0.87 → Precision과 Recall이 균형 잡혀 있음
- 1 (이탈): 0.70 → 이탈 고객 예측 성능이 떨어짐
5.2 Macro avg vs Weighted avg (8에서 개념설명)
- Macro avg: Precision, Recall, F1-score의 단순 평균
- (0.85 + 0.75) / 2 = 0.80
- 모든 클래스가 동일한 중요도를 가짐
- 클래스 샘플 개수가 비슷할 때 유용
- Weighted avg: 각 클래스의 샘플 수를 고려한 가중 평균
- (0.85×400 + 0.75×200) / (400+200) = 0.81
- 클래스 샘플 개수가 다를 때 유용
- 참고
혼동 행렬 예시
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
# 혼동 행렬 계산
cm = confusion_matrix(y_test, y_pred)
# 시각화
plt.figure(figsize=(6, 4))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.title("혼동 행렬 (Confusion Matrix)")
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.show()
출력 예시 (Confusion Matrix)
예측 0 예측 1
실제 0 | TN (4) | FP (6)
실제 1 | FN (1) | TP (89)
이걸 보면, 모델이 어떤 부분에서 잘못된 예측을 했는지 쉽게 알 수 있음!
✔ FN(1) → 실제 전환 고객 1명을 모델이 놓쳤다!
✔ FP(6) → 모델이 전환될 것이라고 예측했지만 실제 미전환된 고객이 6명이다!
- Precision vs. Recall 차이 정리! (이탈여부 예시)
개념 Precision (정밀도) Recall (재현율)
| 의미 | 이탈(1)로 예측한 것 중 실제 이탈 고객 비율 | 실제 이탈 고객 중에서 이탈로 맞춘 비율 |
| 공식 | TP / (TP + FP) | TP / (TP + FN) |
| 초점 | "내가 예측한 게 얼마나 정확해?" | "실제 정답을 놓치지 않고 다 찾았어?" |
| 높을수록 | 오답(FP)이 적고 예측이 정확 | 놓친 이탈(FN)이 적고 정답을 잘 찾음 |
| 낮을수록 | 유지 고객까지 이탈로 오판하는 경우 많음 | 이탈 고객을 많이 놓침 |
| 사용 예시 | 광고 타겟팅, 스팸 필터링 (맞다고 한 게 정확해야 하는 경우) | 암 진단, 금융 사기 탐지 (실제 양성을 놓치면 안 되는 경우) |
- Precision vs. Recall, 어떤 게 더 중요한가?
정확하게 예측해야 하는 상황 (Precision 중요!) ✔ 광고 타겟팅 → 광고비를 줄이기 위해
✔ 스팸 필터 → 정상 메일을 스팸으로 분류하면 안 됨
놓치면 안 되는 상황 (Recall 중요!) ✔ 의료 진단 → 암 환자를 놓치면 안 됨
✔ 금융 사기 탐지 → 사기를 놓치면 안 됨
6. 훈련된 모델의 회귀 계수 해석
로지스틱 회귀에서 coef_는 각 독립 변수가 종속 변수(예측 값)에 미치는 영향력을 나타낸다.
- 로지스틱 회귀는 확률을 예측하는 모델이기 때문에, 회귀 계수가 직접적인 예측 값이 아니라 로그 오즈 비(log-odds)를 의미함.
- 선형 회귀처럼 "1 증가 시 얼마만큼 증가" 이런 식으로 직관적으로 해석하기 어려움.
- 대신 **각 독립 변수가 결과에 미치는 상대적 영향력(비율)**을 파악하는 용도로 사용됨.
import pandas as pd
# 회귀 계수 출력
coef_df = pd.DataFrame({
"Feature": X.columns,
"Coefficient": model.coef_[0]
})
print(coef_df)
출력 예시
Feature Coefficient
0 Watch Time 0.8215
1 Visit Count 0.4178
6.1 회귀 계수 해석
- 광고 시청 시간(Watch Time) → 계수 0.8215→ 큰 양수 값이므로 영향력이 강함
- → 광고 시청 시간이 증가할수록 클릭 확률(전환 확률)이 증가
- 방문 횟수(Visit Count) → 계수 0.4178→ 하지만 광고 시청 시간보다는 영향력이 상대적으로 적음
- → 방문 횟수가 많을수록 클릭 확률 증가
7. 로지스틱 회귀 분석 보고서
그로스 마케팅 보고서: 로지스틱 회귀를 활용한 고객 전환율 분석
1. 개요
본 보고서는 광고 비용, 웹사이트 방문 수, 소셜 미디어 상호작용, 할인 제공 여부가 고객 전환율(Conversion Rate)에 미치는 영향을 분석하기 위해 로지스틱 회귀 모델을 활용하였다. 이를 통해 마케팅 예산을 최적화하고 전환율을 증가시키기 위한 전략을 도출한다.
2. 데이터 개요
- 데이터셋: 고객 전환율 분석 (conversion_rate_analysis.csv)
- 데이터 크기: 500개 샘플
- 변수 정의:
- 광고 비용(Ad Spend, $): 디지털 마케팅에 지출한 광고 비용
- 웹사이트 방문 수(Website Visits): 사용자의 웹사이트 방문 횟수
- 소셜 미디어 상호작용(Social Media Interactions): SNS에서 좋아요, 댓글, 공유 등의 상호작용 횟수
- 할인 제공 여부(Discount Offered, 0 or 1): 할인 제공 여부 (0=할인 없음, 1=할인 제공)
- 전환 여부(Converted, 0 or 1): 고객이 실제 구매를 했는지 여부 (0=미전환, 1=전환)
3. 로지스틱 회귀 분석
- 기본적인 평가 지표 정리: 모델의 전체적인 성능 평가, Precision & Recall 분석
모델 정확도: "모델의 전체 정확도는 93%로 나타남."
Precision (1 기준, 전환 고객 분석): "전환될 가능성이 높은 고객을 94%의 Precision으로 예측 가능."
Recall (1 기준, 전환 고객 분석): "실제 전환된 고객 중 99%를 모델이 맞췄음."
- 혼동 행렬 분석 (잘못된 예측 강조)
FP (잘못된 전환 예측): "모델이 전환될 것이라 예측했지만 실제 전환되지 않은 고객이 6명 존재."
FN (잘못된 비전환 예측): "실제 전환된 고객 중 1명을 모델이 놓침."
- 비즈니스 인사이트: 마케팅 전략, 비용 절감, 전환율 최적화 방안과 연결
Precision(정확도)이 높아 타겟 마케팅 비용을 절감하는 데 활용 가능
Recall이 낮아 일부 전환 고객을 놓칠 가능성이 있으므로, 고객 세그먼트 조정 필요
최종 보고서
"로지스틱 회귀 모델의 정확도는 93%로 나타났다. Precision 94%와 Recall 99%를 기록하여, 전환 가능성이 높은 고객을 매우 효과적으로 식별할 수 있음을 확인하였다.
특히, Precision이 높아 불필요한 마케팅 비용을 줄이는 데 유리하다. 하지만 Recall이 낮은 경우 일부 전환 고객을 놓칠 수 있으므로, 모델 개선이 필요할 수 있다.
혼동 행렬 분석 결과, 모델이 전환될 것이라고 예측한 96명 중 6명이 실제로 전환되지 않았으며, 실제 전환 고객 중 1명을 놓쳤다. 이러한 결과를 기반으로, 모델을 활용한 마케팅 최적화 전략을 마련할 수 있다."



그로스 마케팅 보고서: 로지스틱 회귀를 활용한 고객 재구매율 분석


8. 모델 성능 평가 및 다중 분류 개념
(Day 25에 추가 내용, 새로운 내용만 정리.)
1. 모델 성능 평가 방법
머신러닝 모델을 평가할 때 자주 사용되는 주요 지표
(1) 정확도(Accuracy)
(2) 정밀도(Precision)
(3) 재현율(Recall)
(4) F1-Score
(5) ROC-AUC (Receiver Operating Characteristic - Area Under Curve)
- ROC 곡선은 모델의 분류 성능을 시각적으로 평가하는 방법.
- AUC 값이 1에 가까울수록 모델이 긍정 클래스와 부정 클래스를 잘 구분한다는 의미.
- 임계값(Threshold)에 따라 Precision-Recall이 변화하는 경향을 분석 가능.
2. 다중 분류(Multi-Class Classification)
이진 분류(Binary Classification)는 두 개의 클래스를 구분하는 문제이지만,
다중 분류(Multi-Class Classification) 는 세 개 이상의 클래스를 분류하는 문제이다.
예제:
- 손글씨 숫자 인식 (MNIST 데이터셋) → 0~9까지의 10개 숫자를 분류
- 상품 추천 시스템 → 고객을 여러 구매 성향(High-Spender, Medium-Spender, Low-Spender)으로 분류
(1) 소프트맥스 함수(Softmax Function)
로지스틱 회귀는 이진 분류에서 시그모이드(Sigmoid) 함수를 사용하지만,
다중 분류에서는 소프트맥스(Softmax) 함수를 사용한다. (가장 많이 사용)

- 소프트맥스 함수는 각 클래스에 대한 확률 값을 출력하며, 확률 합은 항상 1이 된다.
- 가장 확률이 높은 클래스를 최종 예측값으로 선택.
(2) One-vs-Rest (OvR) 방식
(3) One-vs-One (OvO) 방식
3. 다중 분류 모델 평가 방법
다중 분류에서도 정확도, Precision, Recall, F1-score 등을 활용하여 모델 성능을 평가할 수 있다.
다만 다중 분류에서는 각 클래스별로 Precision, Recall, F1-score를 구한 후 평균을 내는 방법을 사용한다.
(1) 매크로 평균(Macro Average)
- 각 클래스별 Precision, Recall, F1-score를 계산한 후 평균을 구함.
- 클래스의 샘플 수와 관계없이 동일한 가중치를 부여.
- 클래스 균형이 맞을 때 적절한 평가 방식.
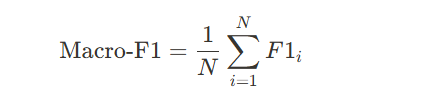
(2) 가중 평균(Weighted Average)
- 클래스별 샘플 수(가중치)를 반영하여 평균을 계산.
- 데이터 불균형이 존재할 때 더 적절한 평가 방식.
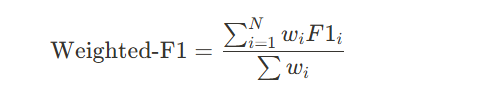
(3) 마이크로 평균(Micro Average)
- 전체 샘플을 기준으로 TP, FP, FN을 합산하여 Precision, Recall, F1-score를 계산.
- 샘플 개수가 많을수록 더 높은 비중을 반영.
로지스틱 회귀(Logistic Regression)를 이용한 다중 분류(Multiclass Classification) 코드
기업이 고객을 대상으로 온라인 마케팅 캠페인을 진행하고 있다. 각 고객의 나이, 소비 점수, 광고 클릭률, 이메일 오픈율을 바탕으로 고객이 해당 캠페인에 얼마나 적극적으로 반응할지(High, Medium, Low) 예측하는 모델을 개발한다. 이 모델을 활용하여 타겟 고객을 분류하고 맞춤형 마케팅 전략을 수립할 수 있다.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, LabelEncoder
from sklearn.linear_model import LogisticRegression
# 1. 가상의 마케팅 데이터 생성
data = {
'age': [22, 45, 25, 47, 35, 50, 29, 41, 60, 33, 39, 28, 42, 23, 37],
'spending_score': [80, 55, 90, 40, 70, 35, 85, 50, 20, 75, 65, 88, 45, 95, 60],
'ad_click_rate': [0.9, 0.3, 0.8, 0.2, 0.7, 0.1, 0.85, 0.4, 0.05, 0.75, 0.6, 0.88, 0.35, 0.92, 0.5],
'email_open_rate': [0.95, 0.4, 0.9, 0.3, 0.75, 0.2, 0.89, 0.5, 0.1, 0.78, 0.65, 0.91, 0.37, 0.96, 0.55],
'engagement_level': ['High', 'Medium', 'High', 'Low', 'High', 'Low', 'High', 'Medium', 'Low',
'High', 'Medium', 'High', 'Medium', 'High', 'Medium']
}
df = pd.DataFrame(data)
# 2. 독립변수(X)와 종속변수(y) 설정
X = df[['age', 'spending_score', 'ad_click_rate', 'email_open_rate']]
y = df['engagement_level']
# 3. 라벨 인코딩 (문자 → 숫자 변환)
label_encoder = LabelEncoder()
y_encoded = label_encoder.fit_transform(y)
# 4. 데이터 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 5. 훈련/테스트 데이터 분할 (7:3 비율)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_encoded, test_size=0.3, random_state=42, stratify=y_encoded)
# 6. 로지스틱 회귀 모델 훈련 (다중 분류)
model = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)
model.fit(X_train, y_train)
# 7. 테스트 데이터 예측
y_pred = model.predict(X_test)
# 8. 예측 결과 출력
print("테스트 데이터 예측 결과:")
for i, pred in enumerate(y_pred):
print(f"테스트 데이터 {i+1}: 예측된 참여 수준 - {label_encoder.inverse_transform([pred])[0]}")
- 기업은 고객의 행동 패턴을 분석하여 적극적인 반응을 보일 고객층(High Engagement) 을 대상으로 집중적인 마케팅 전략을 수행할 수 있다.
- 반대로, 반응이 낮은 고객층(Low Engagement) 에게는 보다 효과적인 광고 소재나 재참여 유도 전략을 제공할 수 있다.
'STUDY' 카테고리의 다른 글
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 27-1 인공신경망 ANN (1) | 2025.03.14 |
|---|---|
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 26 kNN, SVM, 로지스틱 회귀 실습 (0) | 2025.03.13 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 23 선형 회귀분석 복습, 실습 (2) | 2025.03.10 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day22 머신러닝 기초, 로지스틱 회귀 실습 (0) | 2025.03.07 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day21 루커 스튜디오 실습, chart.js 웹 서비스 (1) | 2025.03.07 |



