1. ANN 개요
(1) 인공신경망(ANN)란?
- 인간의 뇌를 모방한 머신러닝 모델.
- 데이터에서 패턴을 학습하여 분류(Classification)와 예측(Regression) 수행.
- 입력층 (→ 은닉층 )→ 출력층 구조.
(2) ANN의 핵심 개념
뉴런(Neuron) (노드)
- 입력 → 계산(가중치 곱, 활성화 함수 적용) → 출력
- 뇌의 뉴런(Neuron)처럼 데이터 신호를 전달함.
레이어(Layer) (층)
- 입력층(Input Layer): 원본 데이터를 입력받음.
- 은닉층(Hidden Layer): 데이터의 중요한 특징을 추출.
- 출력층(Output Layer): 최종 결과를 출력.
가중치(Weight)와 편향(Bias)
- 가중치(Weight): 뉴런 간 연결 강도를 결정하는 값.
- 편향(Bias): 추가적인 조정값으로, 뉴런의 활성화 정도를 조절.
활성화 함수(Activation Function)
- 비선형성을 추가하여 복잡한 패턴을 학습할 수 있도록 도와줌.
- 주요 활성화 함수:
- ReLU (Rectified Linear Unit): 가장 많이 사용됨. 값이 0 이하면 0, 0 초과면 그대로 유지.
- Sigmoid: 0~1 사이 값 출력, 확률 예측에 유용.
- Softmax: 다중 분류 문제에서 사용.
(출력노드가 하나면 회귀, (어떤일의 확률을 구할때. 확률 예측))
(순서대로 ReLU, Sigmoid, hyperbolic)




AF: 활성화 함수, $\mathbf{b}^{(0)}$ : 편향, W: 가중치
2. ANN의 구조
(1) 단층 퍼셉트론 (SLP, Single Layer Perceptron)
- 입력층과 출력층만 존재.
- 선형 문제 해결 가능 (예: AND, OR 문제)
- XOR 문제 해결 불가능 → 해결을 위해 다층 신경망(MLP) 필요.


✔ Python 코드
import numpy as np
# 시그모이드 활성화 함수
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# SLP 구현 (하드 코딩된 가중치와 편향) 단일층 퍼셉트론 함수
def forward_slp(X, W, b): #순방향 함수(입력, 가중치, 절편)
Z = np.dot(W, X) + b # 선형 변환, 회귀식 형태로 계산
A = sigmoid(Z) # 시그모이드 활성화 함수 적용
return A
# 입력 데이터 예시 (특징 3개)
X = np.array([[1], [2], [3]]) # 입력 데이터
# 하드코딩된 가중치와 편향
W = np.array([[0.2, 0.4, 0.6]]) # 1x3 크기 (하나의 노드), 노드별로 가중치 입력
b = np.array([[0.5]]) # 편향
# SLP 순전파 실행
output_slp = forward_slp(X, W, b)
#결과 출력
print("Single Layer Perceptron 출력:", output_slp)
#출력값
Single Layer Perceptron 출력: [[0.96442881]]
(2) 다층 퍼셉트론 (MLP, Multi-Layer Perceptron)
- 은닉층 추가 → 비선형 문제(XOR 등) 해결 가능.
- 3개 이상의 은닉층이 있는 경우 "딥러닝(Deep Learning)" 이라고 함.
- ReLU 활성화 함수를 은닉층에 적용, 출력층에서는 Softmax 사용.
✔ 수식 1️⃣ 첫 번째 은닉층
$z(1)= W(1)x+b(1)a(1)=f(z(1))(ReLU 사용)$
2️⃣ 출력층
$z(2)=W(2)a(1)+b(2)y^=Softmax(z(2))$
✔ Python 코드
# ReLU 활성화 함수
def relu(z):
return np.maximum(0, z)
# 소프트맥스 함수
def softmax(z):
exp_z = np.exp(z - np.max(z)) # 안정성을 위한 처리
return exp_z / np.sum(exp_z, axis=0)
# MLP 구현 (하드 코딩된 가중치와 편향)
def forward_mlp(X, parameters):
# 첫 번째 은닉층
W1 = parameters['W1']
b1 = parameters['b1']
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 출력층
W2 = parameters['W2']
b2 = parameters['b2']
Z2 = np.dot(W2, A1) + b2
A2 = softmax(Z2)
return A2
# 입력 데이터 예시 (특징 3개)
X = np.array([[1], [2], [3]]) # 입력 데이터
# 하드코딩된 가중치와 편향
parameters = {
'W1': np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6], [0.7, 0.8, 0.9], [1.0, 1.1, 1.2]]), # 은닉층 가중치 (4x3)
'b1': np.array([[0.1], [0.2], [0.3], [0.4]]), # 은닉층 편향 (4x1)
'W2': np.array([[0.1, 0.2, 0.3, 0.4], [0.5, 0.6, 0.7, 0.8]]), # 출력층 가중치 (2x4)
'b2': np.array([[0.1], [0.2]]) # 출력층 편향 (2x1)
}
# MLP 순전파
output_mlp = forward_mlp(X, parameters)
print("Multi-Layer Perceptron 출력:", output_mlp)
#출력값
Multi-Layer Perceptron 출력: [[8.58041227e-04]
[9.99141959e-01]]
3. ANN 학습 과정
ANN이 데이터를 학습하는 과정은 크게 순전파 → 손실 계산 → 역전파 → 가중치 업데이트로 나뉨.
(1) 순전파 (Forward Propagation)
입력 데이터를 네트워크에 전달하여 예측값을 계산하는 과정
- 데이터를 입력층 → 은닉층 → 출력층으로 전달하면서 연산 수행.
- 각 층에서 가중치 적용 → 활성화 함수 적용 → 다음 층으로 전달.
✔ 수식$z=W⋅x+ba=f(z)$
1️⃣ 첫 번째 은닉층
$z(1)=W(1)x+b(1)z^{(1)} = W^{(1)} x + b^{(1)}a(1)=f(z(1))(활성화 함수 적용, 예: ReLU)$
2️⃣ 출력층
$z(2)=W(2)a(1)+b(2)z^{(2)} = W^{(2)} a^{(1)} + b^{(2)}y^=Softmax(z(2))$
✔ Python 코드 (순전파)
import numpy as np
def relu(z):
return np.maximum(0, z)
def softmax(z):
exp_z = np.exp(z - np.max(z)) # Overflow 방지
return exp_z / np.sum(exp_z, axis=0)
def forward_propagation(X, parameters):
W1, b1, W2, b2 = parameters['W1'], parameters['b1'], parameters['W2'], parameters['b2']
# 은닉층
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 출력층
Z2 = np.dot(W2, A1) + b2
A2 = softmax(Z2)
return A2
✔ 순전파 핵심 정리
- 입력 데이터에 가중치 곱하고 편향 더함 → Z 값 생성
- 활성화 함수 적용하여 비선형 변환 → A 값 생성
- 마지막 출력층에서는 Softmax를 적용해 확률 값 예측
(2) 손실 함수 (Loss Function)
순전파를 거친 예측값과 실제값의 차이를 측정하는 단계
- 손실(loss)이 작을수록 모델이 잘 학습된 것!
- 대표적인 손실 함수:
- MSE(Mean Squared Error, 평균제곱오차) → 회귀 문제에 주로 사용.
- Cross-Entropy Loss → 분류 문제에서 사용.
✔ MSE 수식
$L = \frac{1}{2} (y - a)^2$
$L$ 손실 함수, y 실제값, a 예측값
✔ Python 코드
def mse_loss(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
(3) 역전파 (Backpropagation) (= 오차역전파)
각 가중치 $W$ 에 대한 손실 함수 $L$ 의 기울기를 계산하는 과정입니다.
출력과 실제 값의 차이로부터 가중치에 대한 기울기를 계산하고, 이를 사용해 가중치를 업데이트합니다.
- 연쇄법칙(Chain Rule) 을 이용해 미분하여 가중치의 기울기(Gradient)를 계산.
✔ 수식
- 출력층의 기울기 계산
$dL/dz(2)=y^−y$
- 은닉층의 기울기 계산 (ReLU 활성화 함수)
$dL/dz(1)=(W(2))T⋅dL/dz(2)⋅f′(z(1))$
- 가중치 업데이트
$W_{\text{new}} = W_{\text{old}} - \eta \cdot \frac{\partial L}{\partial W}$
여기서 $\eta$ 는 학습률입니다.
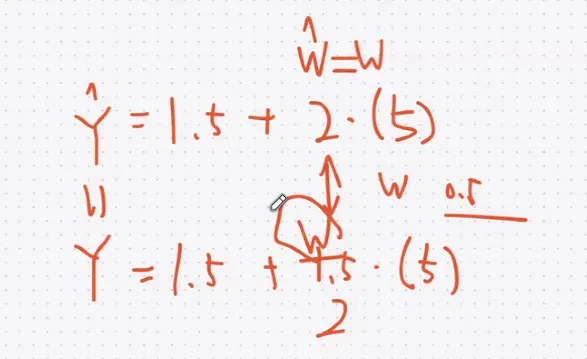
색 비율을 조정하는 것처럼 점점 조정해서 같게함
✔ Python 코드 (역전파)
def backward_propagation(X, Y, parameters, cache):
m = X.shape[1] # 샘플 수
grads = {}
# 출력층 오차
A3 = cache['A3']
dZ3 = A3 - Y
grads['dW3'] = np.dot(dZ3, cache['A2'].T) / m
grads['db3'] = np.sum(dZ3, axis=1, keepdims=True) / m
# 은닉층 오차
dA2 = np.dot(parameters['W3'].T, dZ3)
dZ2 = dA2 * (cache['Z2'] > 0) # ReLU 미분 적용
grads['dW2'] = np.dot(dZ2, cache['A1'].T) / m
grads['db2'] = np.sum(dZ2, axis=1, keepdims=True) / m
return grads
✔ 역전파 핵심 정리
- 출력층 → 손실과 예측 값 차이 계산
- 은닉층 → 연쇄법칙을 사용해 가중치의 기울기 계산
- 각 레이어의 가중치를 업데이트하여 학습 진행
(4) 경사하강법 (Gradient Descent)
역전파를 통해 학습률에 따라 계산한 기울기를 이용해 가중치를 업데이트하는 알고리즘
- 목표: 손실 함수를 최소화하는 최적의 가중치 찾기.
✔ 수식W=W−η⋅∂L∂WW = W - \eta \cdot \frac{\partial L}{\partial W}
(η는 학습률, Learning Rate)
✔ Python 코드
def update_parameters(parameters, grads, learning_rate):
for l in range(1, len(parameters) // 2 + 1):
parameters['W' + str(l)] -= learning_rate * grads['dW' + str(l)]
parameters['b' + str(l)] -= learning_rate * grads['db' + str(l)]
return parameters
✔ 경사하강법 핵심 정리
- 기울기가 큰 방향으로 가중치를 이동하여 손실을 줄임
- 학습률(η)이 너무 크면 불안정, 너무 작으면 학습이 느려짐
- 확률적 경사 하강법(SGD), Adam Optimizer 등 다양한 변형이 존재
- 처음에는 랜덤하게 가중치를 초기화하지만, 이후에는 기울기를 따라 이동하면서 가중치를 업데이트함.
- 기울기가 0이 되는 지점이 손실이 최소가 되는 지점이고, 그때 학습이 종료됨.
- 모든 데이터에 대해 미분을 계산해야 하므로, 연산량이 많아질 수 있음.
정리
과정 설명
| 순전파 | 입력 → 가중치 곱 → 활성화 함수 적용 → 예측값 출력 |
| 손실 계산 | 예측값과 실제값의 차이를 측정 |
| 역전파 | 손실을 줄이기 위해 가중치의 기울기 계산 |
| 경사하강법 | 기울기를 따라 가중치 업데이트하여 학습 진행 |
✅ 순전파 → 손실 계산 → 역전파 → 경사하강법
➡ 이 과정이 반복되면서 ANN이 점점 더 정확한 예측을 수행하게 됨!
자세한 설명 접는글( 손실계산의 활용)
- ✅ 손실 함수(MSE)와 가중치 업데이트 과정
- 출력층에서 손실 계산
- 모델이 예측한 값(a)과 실제값(y)의 차이를 계산함.
- MSE를 사용해서 오차의 크기를 측정.
- 예를 들어, 실제값이 10이고 예측값이 8이면 손실은:
- $L = (10 - 8)^2 = 4$
- 이 손실 값을 최소화하기 위해 가중치를 업데이트해야 함.
- 역전파(Backpropagation)를 통해 가중치 기울기 계산
- 손실 함수 L 을 가중치 W에 대해 미분하여 기울기(Gradient)를 구함.
- 기울기가 크다는 것은 손실이 크다는 의미이므로, 가중치를 조정해서 손실을 줄여야 함.
- 연쇄법칙을 사용하여 각 층의 가중치에 대한 변화량을 계산함.
- 경사하강법(Gradient Descent)으로 가중치 업데이트
- 손실을 줄이기 위해 가중치를 반대 방향으로 조금씩 수정.
- 학습률(learning rate, $η$)을 곱해서 적절한 크기로 업데이트함.
- $W_{\text{new}} = W_{\text{old}} - \eta \cdot \frac{\partial L}{\partial W}$
- 여기서 $\frac{\partial L}{\partial W}$는 MSE를 가중치W 에 대해 미분한 값.
- 학습률이 너무 크면 진동하고, 너무 작으면 학습이 느려짐.
- Epoch마다 손실 함수 값 감소
- Epoch(에포크): 전체 데이터를 한 번 학습하는 과정.
- 여러 epoch 동안 가중치를 조정하면서 MSE 값이 점점 줄어들게 됨.
- 학습이 잘 되면 손실 함수 값이 점차 0에 가까워짐.
- 예를 들어:
- Epoch 1: Loss = 4.5 Epoch 2: Loss = 3.2 Epoch 3: Loss = 2.1 ... Epoch 100: Loss = 0.1
- 손실 함수가 최소값에 도달하면 최적의 가중치를 찾은 것.
- 최적의 가중치로 예측값 도출
- 학습이 끝난 후, 새로운 데이터를 입력하면 최적의 가중치를 사용해서 예측값을 도출.
- 예를 들어, 새로운 입력값이 들어오면:
- $y_{\text{pred}} = W_{\text{final}} \cdot X + b$
- MSE가 최소화된 상태이므로 예측값이 실제값과 가장 가깝게 나옴.
✅ 한 줄 요약 - 출력층에서 손실 계산
- MSE는 손실을 측정하는 함수이고, 이를 이용해 가중치를 조정하면서 손실이 점점 작아지도록(epoch마다 감소) 학습하는 것이 신경망 학습의 핵심 원리야. 🔥
4. 코드 예시
- 필요한 라이브러리 불러오기
import numpy as np
- 활성화 함수 정의
은닉층에서 주로 사용되는 활성화 함수인 ReLU와 출력층에 적용되는 소프트맥스 함수를 정의합니다.
# ReLU 활성화 함수 정의
def relu(z):
return np.maximum(0, z)
# 소프트맥스 함수 정의
def softmax(z):
exp_z = np.exp(z - np.max(z)) # Overflow 방지를 위해 최대값을 뺌
return exp_z / np.sum(exp_z, axis=0)
- 신경망 가중치 초기화
가중치 $\mathbf{W}$ 와 편향 $\mathbf{b}$ 를 초기화합니다. 랜덤 초기화를 사용합니다.
# 가중치 및 편향 초기화 함수 (랜덤)
def initialize_parameters(layer_dims):
np.random.seed(1)
parameters = {}
L = len(layer_dims) # 층의 개수
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
return parameters
layer_dims는 각 층의 뉴런 수를 정의한 리스트입니다. 예를 들어, 입력층 3개 뉴런, 첫 번째 은닉층 4개 뉴런, 두 번째 은닉층 5개 뉴런, 출력층 3개 뉴런이라면 layer_dims = [3, 4, 5, 3]로 설정합니다.
- 순전파 (Forward Propagation) 구현
입력 데이터에 대해 순전파 과정을 구현합니다. 각 은닉층에서는 가중합을 계산하고 활성화 함수를 적용합니다. 최종 출력층에서는 소프트맥스를 적용하여 확률을 반환합니다.
def forward_propagation(X, parameters):
# 첫 번째 은닉층
W1 = parameters['W1']
b1 = parameters['b1']
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 두 번째 은닉층
W2 = parameters['W2']
b2 = parameters['b2']
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
# 출력층
W3 = parameters['W3']
b3 = parameters['b3']
Z3 = np.dot(W3, A2) + b3
A3 = softmax(Z3) # 소프트맥스 적용
return A3
여기서:
- X는 입력 데이터(특징 벡터)입니다.
- Z1, Z2, Z3는 각 층에서의 가중합을 의미합니다.
- A1, A2, A3는 각 층의 활성화 함수의 출력을 의미합니다.
- 사용 예시
다음은 신경망의 각 층을 정의하고, 데이터를 입력하여 순전파를 수행하는 과정을 설명합니다.
# 입력 데이터 예시 (특징 수 3, 샘플 수 1)
X = np.array([[1], [2], [3]])
# 각 층의 뉴런 수를 정의 (입력층 3개, 은닉층 4개, 5개, 출력층 3개)
layer_dims = [3, 4, 5, 3]
# 가중치 및 편향 초기화
parameters = initialize_parameters(layer_dims)
# 순전파 실행
output = forward_propagation(X, parameters)
# 출력 결과
print("Softmax 확률 출력:", output)
- 위 코드에 대한 통합 코드
import numpy as np
# ReLU 활성화 함수 정의
def relu(z):
return np.maximum(0, z)
# 소프트맥스 함수 정의
def softmax(z):
exp_z = np.exp(z - np.max(z)) # Overflow 방지를 위해 최대값을 뺌
return exp_z / np.sum(exp_z, axis=0)
# 가중치 및 편향 초기화 함수 (랜덤)
def initialize_parameters(layer_dims):
np.random.seed(1)
parameters = {}
L = len(layer_dims) # 층의 개수
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
return parameters
# 순전파 (Forward Propagation) 구현
def forward_propagation(X, parameters):
# 첫 번째 은닉층
W1 = parameters['W1']
b1 = parameters['b1']
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 두 번째 은닉층
W2 = parameters['W2']
b2 = parameters['b2']
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
# 출력층
W3 = parameters['W3']
b3 = parameters['b3']
Z3 = np.dot(W3, A2) + b3
A3 = softmax(Z3) # 소프트맥스 적용
return A3
# 사용 예시
# 입력 데이터 예시 (특징 수 3, 샘플 수 1)
X = np.array([[1], [2], [3]])
# 각 층의 뉴런 수를 정의 (입력층 3개, 은닉층 4개, 5개, 출력층 3개)
layer_dims = [3, 4, 5, 3]
# 가중치 및 편향 초기화
parameters = initialize_parameters(layer_dims)
# 순전파 실행
output = forward_propagation(X, parameters)
# 출력 결과
print("Softmax 확률 출력:", output)
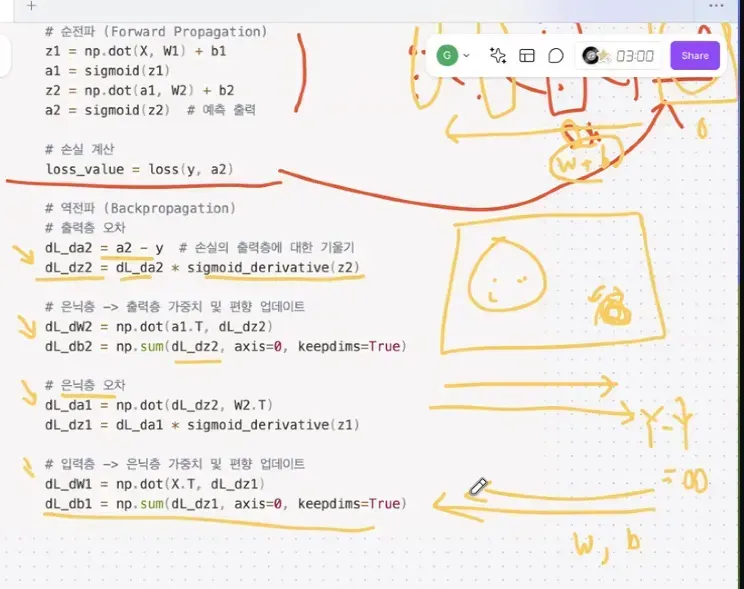
- 다층신경망을 적용한 매출예측
import numpy as np
# ReLU 활성화 함수 정의
def relu(z):
return np.maximum(0, z)
# ReLU 미분 함수 (Backpropagation에서 사용)
def relu_derivative(z):
return np.where(z > 0, 1, 0)
# 손실 함수 (Mean Squared Error)
def compute_loss(Y, A):
m = Y.shape[1] # 샘플 수
loss = np.mean((Y - A) ** 2) # MSE 계산
return loss
# 가중치 및 편향 초기화 함수
def initialize_parameters(layer_dims):
np.random.seed(1)
parameters = {}
for l in range(1, len(layer_dims)):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
return parameters
# 순전파 (Forward Propagation)
def forward_propagation(X, parameters):
cache = {}
# 첫 번째 은닉층
W1 = parameters['W1']
b1 = parameters['b1']
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 두 번째 은닉층
W2 = parameters['W2']
b2 = parameters['b2']
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
# 출력층 (회귀 문제이므로 활성화 함수 없음)
W3 = parameters['W3']
b3 = parameters['b3']
Z3 = np.dot(W3, A2) + b3
A3 = Z3 # 출력층 활성화 함수는 사용하지 않음
# 캐시 저장 (역전파에서 사용)
cache['Z1'], cache['A1'] = Z1, A1
cache['Z2'], cache['A2'] = Z2, A2
cache['Z3'], cache['A3'] = Z3, A3
return A3, cache
# 역전파 (Backward Propagation)
def backward_propagation(X, Y, parameters, cache):
m = X.shape[1] # 샘플 수
grads = {}
# 출력층 오차
A3 = cache['A3']
dZ3 = A3 - Y
grads['dW3'] = np.dot(dZ3, cache['A2'].T) / m
grads['db3'] = np.sum(dZ3, axis=1, keepdims=True) / m
# 두 번째 은닉층 오차
dA2 = np.dot(parameters['W3'].T, dZ3)
dZ2 = dA2 * relu_derivative(cache['Z2'])
grads['dW2'] = np.dot(dZ2, cache['A1'].T) / m
grads['db2'] = np.sum(dZ2, axis=1, keepdims=True) / m
# 첫 번째 은닉층 오차
dA1 = np.dot(parameters['W2'].T, dZ2)
dZ1 = dA1 * relu_derivative(cache['Z1'])
grads['dW1'] = np.dot(dZ1, X.T) / m
grads['db1'] = np.sum(dZ1, axis=1, keepdims=True) / m
return grads
# 파라미터 업데이트 (경사 하강법)
def update_parameters(parameters, grads, learning_rate):
for l in range(1, len(parameters) // 2 + 1):
parameters['W' + str(l)] -= learning_rate * grads['dW' + str(l)]
parameters['b' + str(l)] -= learning_rate * grads['db' + str(l)]
return parameters
# 학습 데이터 생성 (하드코딩된 연도별 매출 데이터)
X_train = np.array([[2017, 2018, 2019, 2020, 2021]]) # 연도
Y_train = np.array([[100, 150, 200, 250, 300]]) # 해당 연도의 매출
# 데이터 정규화
X_train = X_train / 2021 # 연도를 최대값으로 나누어 정규화
Y_train = Y_train / 300 # 매출도 최대값으로 나누어 정규화
# 레이어 구성 (입력층 1, 은닉층 2개, 출력층 1개)
layer_dims = [1, 5, 3, 1]
# 파라미터 초기화
parameters = initialize_parameters(layer_dims)
# 학습 하이퍼파라미터
learning_rate = 0.01
num_iterations = 10000
# 학습 과정
for i in range(num_iterations):
# 순전파
A3, cache = forward_propagation(X_train, parameters)
# 손실 계산
loss = compute_loss(Y_train, A3)
# 역전파
grads = backward_propagation(X_train, Y_train, parameters, cache)
# 파라미터 업데이트
parameters = update_parameters(parameters, grads, learning_rate)
# 1000번마다 손실 출력
if i % 1000 == 0:
print(f"Iteration {i}, Loss: {loss:.4f}")
# 테스트 데이터 예측
X_test = np.array([[2022]]) # 테스트 데이터 (2022년)
X_test = X_test / 2021 # 정규화
# 순전파로 예측
A3_test, _ = forward_propagation(X_test, parameters)
# 예측 결과 출력 (2022년 매출 예측)
print("2022년 매출 예측 (원래 값):", A3_test * 300) # 원래 단위로 변환
#출력값
Iteration 0, Loss: 0.5000
Iteration 1000, Loss: 0.0556
Iteration 2000, Loss: 0.0556
Iteration 3000, Loss: 0.0556
Iteration 4000, Loss: 0.0556
Iteration 5000, Loss: 0.0556
Iteration 6000, Loss: 0.0556
Iteration 7000, Loss: 0.0556
Iteration 8000, Loss: 0.0556
Iteration 9000, Loss: 0.0556
2022년 매출 예측 (원래 값): [[200.00000233]]
5. 신경망(ANN) vs 심층 신경망(DNN)
구분 신경망(ANN) 심층 신경망(DNN)
| 은닉층 | 1개 이하 | 여러 개(보통 3개 이상) |
| 복잡성 | 단순한 문제 해결 | 복잡한 문제 해결에 유리 |
| 계산 비용 | 낮음 | 매우 높음 |
| 학습 시간 | 짧음 | 길고 많은 데이터가 필요 |
심층 신경망(Deep Neural Network, DNN)
- 구조: 심층 신경망은 여러 개의 은닉층을 가지는 신경망을 의미합니다. 일반적으로 3개 이상의 은닉층을 가진 신경망을 심층 신경망이라고 합니다.
- 특징: 은닉층의 수가 많아질수록 데이터의 복잡한 패턴을 더 잘 학습할 수 있습니다. 각 은닉층은 이전 층에서 입력받은 신호를 비선형 변환을 통해 다음 층으로 전달하면서 데이터를 점점 더 추상적인 수준으로 표현합니다.
- 딥러닝(Deep Learning)이라는 용어는 심층 신경망을 이용한 학습 방법을 가리키며, 심층 신경망은 이미지 처리(CNN, Convolutional Neural Network), 시계열 데이터 처리(RNN, Recurrent Neural Network), 자연어 처리 등에 널리 사용됩니다.
6. 다층신경망 기반 분류모델 연습
- 다층신경망사용 개 vs. 고양이 이미지 분류 모델
- 다층신경망 사용 매출예측
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
# 1. 하드코딩된 매출 데이터 생성 (30년간의 매출 데이터)
years = np.arange(1991, 2021) # 1991년부터 2020년까지의 30년간 데이터
sales = np.array([120, 135, 160, 180, 190, 220, 240, 260, 280, 300, 320, 350, 370, 390, 410,
430, 450, 470, 480, 500, 520, 530, 540, 560, 580, 600, 620, 640, 660, 680]) # 매출 데이터
# 2. 매출에 영향을 줄 수 있는 변수 생성
marketing_spend = np.array([80, 85, 90, 95, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200,
210, 220, 230, 240, 250, 260, 270, 280, 290, 300, 310, 320, 330, 340, 350]) # 마케팅 비용
economy_index = np.array([1.0, 1.1, 0.9, 1.2, 1.0, 0.8, 1.1, 1.0, 0.9, 1.2, 1.0, 1.1, 1.0, 0.9, 1.2,
1.0, 0.8, 1.1, 1.0, 0.9, 1.2, 1.0, 1.1, 1.0, 0.9, 1.2, 1.0, 0.9, 1.2, 1.0]) # 경제 지수
# 3. 데이터를 Pandas DataFrame으로 처리
data = pd.DataFrame({
'Year': years,
'Sales': sales,
'Marketing_Spend': marketing_spend,
'Economy_Index': economy_index
})
print(data.head()) # 데이터 미리보기
# 4. 입력 변수(X)와 출력 변수(y)를 정의
X = data[['Year', 'Marketing_Spend', 'Economy_Index']].values # 연도, 마케팅 비용, 경제 지수
y = data['Sales'].values # 매출
# 5. 데이터 정규화 (입력 데이터 스케일 조정)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # X 데이터를 정규화
# 6. 다층 신경망 모델 정의
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(X_scaled.shape[1],))) # 은닉층 1 (뉴런 128개로 증가)
model.add(Dense(64, activation='relu')) # 은닉층 2 (뉴런 64개로 증가)
model.add(Dense(32, activation='relu')) # 은닉층 3 추가 (뉴런 32개)
model.add(Dense(1)) # 출력층 (매출 예측)
# 7. 모델 컴파일 (learning_rate를 조정)
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001) # 학습률 0.001로 설정
model.compile(optimizer=optimizer, loss='mean_squared_error')
# 8. 모델 학습 (Epochs와 Batch Size를 조정)
model.fit(X_scaled, y, epochs=500, batch_size=10, verbose=1) # 에포크 수 증가, 배치 크기 감소
# 9. 모델 성능 측정 (R² 값 계산)
y_pred = model.predict(X_scaled)
# R² 계산
r2 = r2_score(y, y_pred)
print(f"R² 값: {r2:.4f}")
# 10. 특정 연도의 매출 예측
def predict_sales(year, marketing_spend, economy_index):
# 예측할 데이터를 정규화
input_data = np.array([[year, marketing_spend, economy_index]])
input_data_scaled = scaler.transform(input_data)
# 예측 수행
predicted_sales = model.predict(input_data_scaled)
return predicted_sales[0][0]
# 예시: 2025년의 매출 예측
predicted_sales_2025 = predict_sales(2025, 360, 1.05)
print(f"2025년 예측 매출: {predicted_sales_2025:.2f}")
- 주식정보를 불러와서 특정 날짜의 주식 종가 예측 모델
+경제지수를 반영한 다층신경망 예측
- Google teachable machine으로 모델을 학습하고 GCP VM에서 테스트 & 웹발행
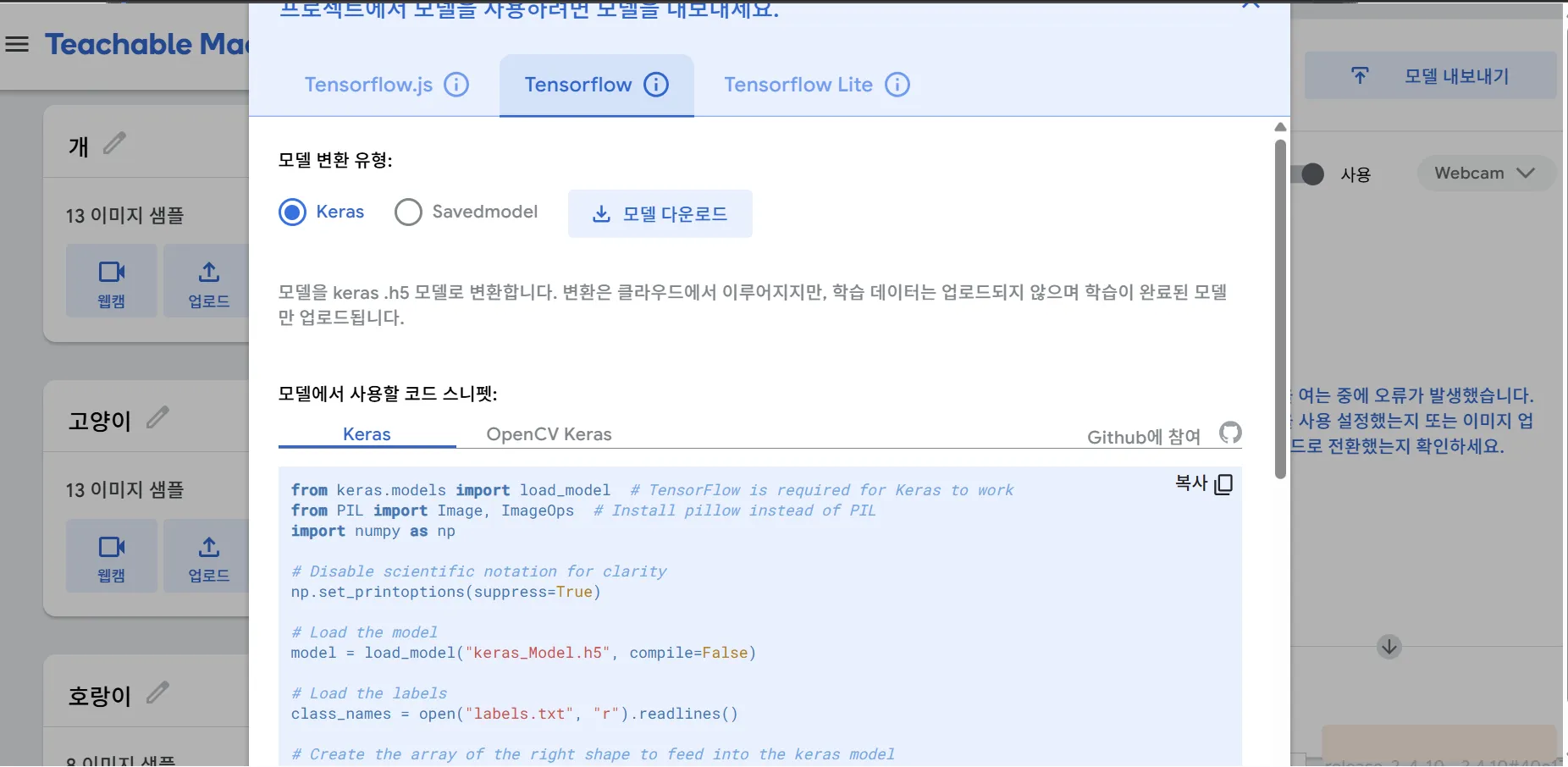
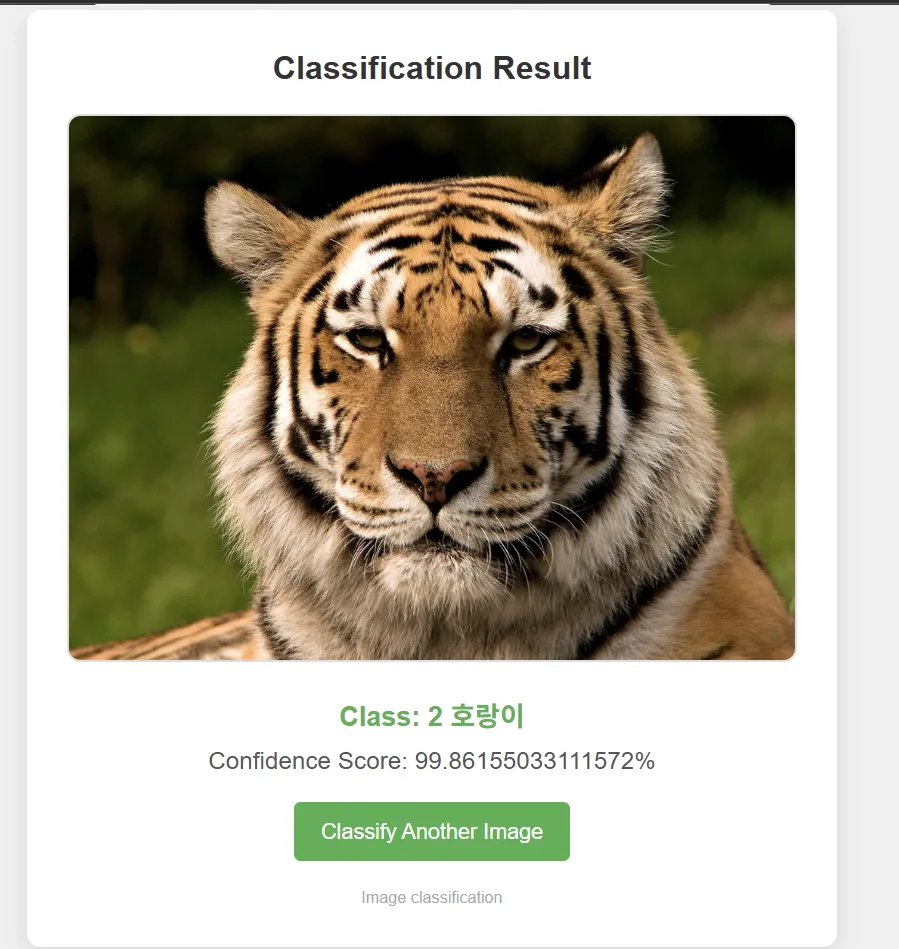
tensorflow로 다운로드 후 app.py랑 html 파일들이랑 같이 넣어주면 됨.
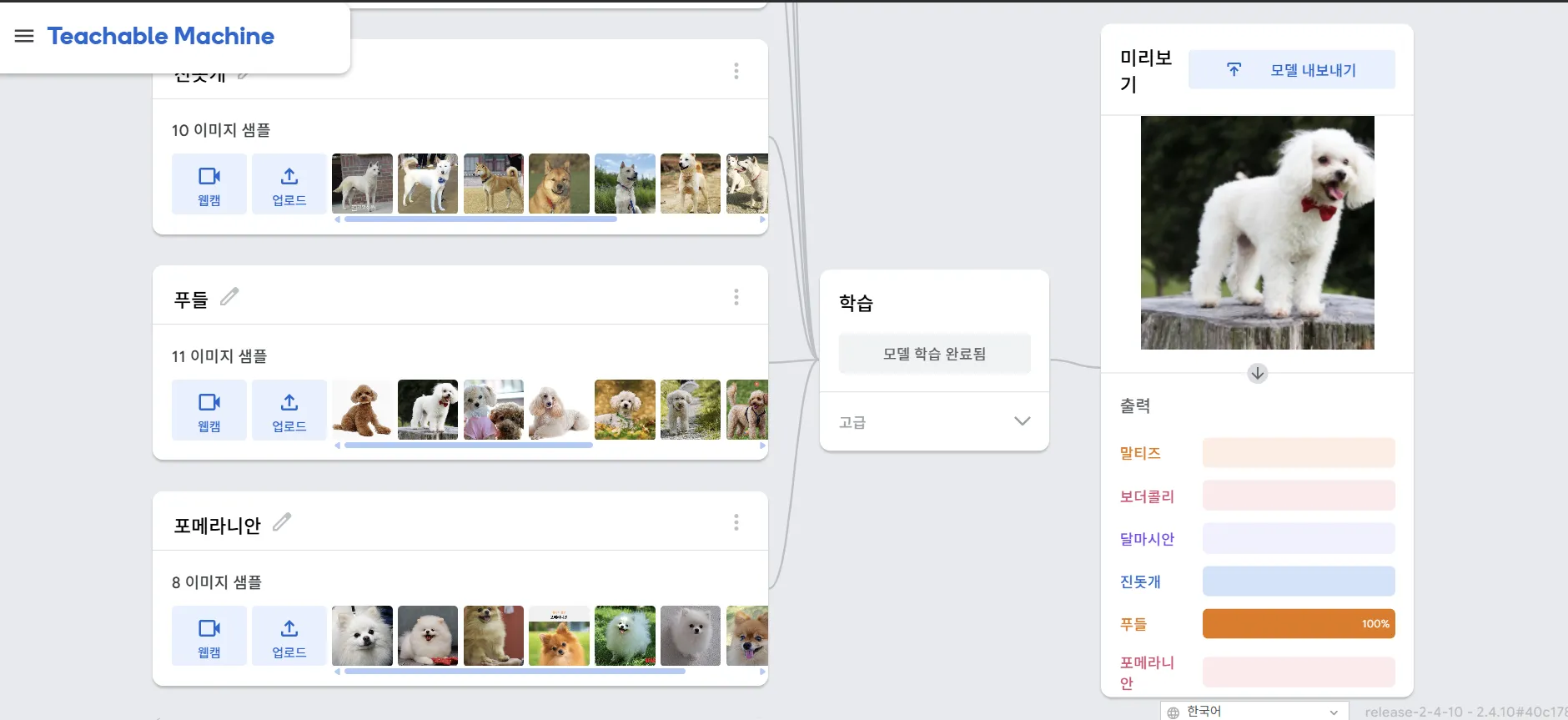
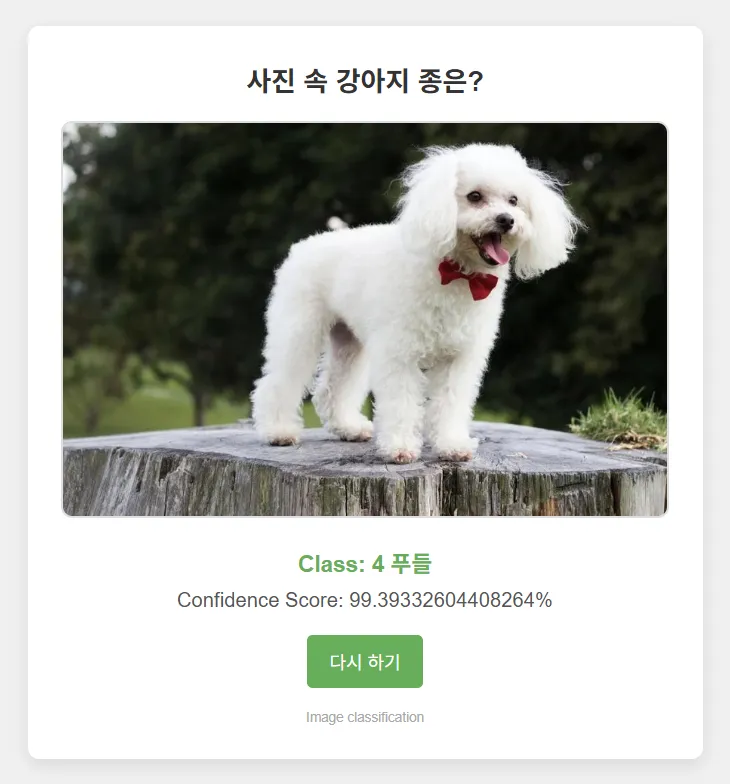
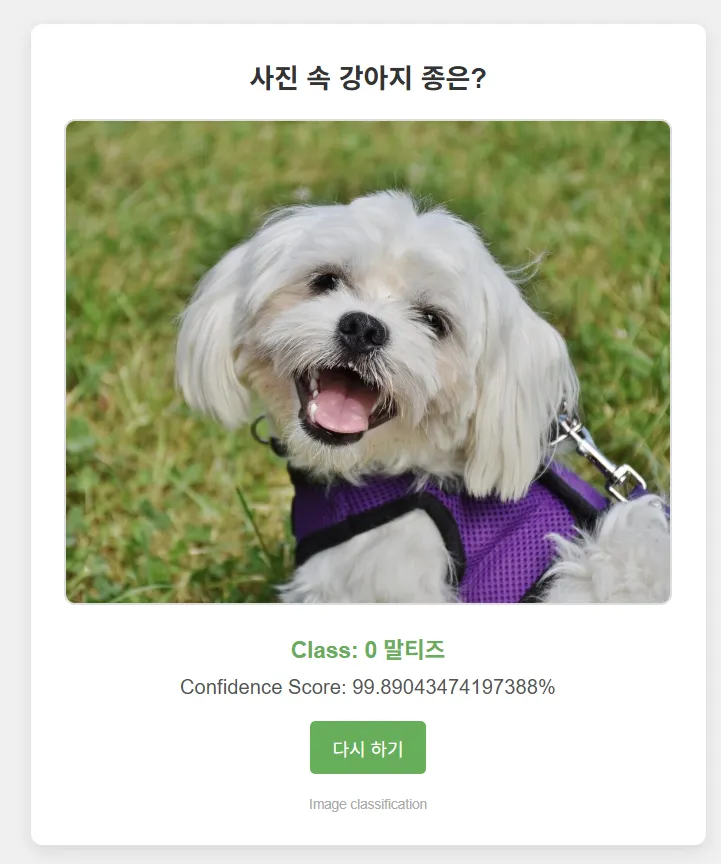
4-1 다중클래스(6개) 예측 모델
티쳐블머신이 CNN 기반이라 성능이 괜찮다고 하셔서 성능이 얼마나인지 궁금해졌고,
+ 실제로 사람들이 사용할만한 웹서비스 모델을 만들고 싶었음.
그래서 탄생한 강아지 도감!
나도 헷갈리는 말티즈, 포메라니안, 푸들 구분을 해냈다!
하다보니 왜 AI에서 학습데이터가 중요한지랑 왜 무단학습이 문제인지 더 실감하게 되었다..
회고
오늘은 인공신경망까지만 하렵니다
다행히 자동목차가 잘 먹었네요 ㅎㅎ
예측 모델이 너무 많아요... 분류 회귀 다중 클래스 손실 함수...
금토일에 하겠읍니다. 화이팅
'STUDY' 카테고리의 다른 글
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 27-2 K-Means Clustering (1) | 2025.03.15 |
|---|---|
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 26 kNN, SVM, 로지스틱 회귀 실습 (0) | 2025.03.13 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 24 로지스틱 회귀, 실습 (1) | 2025.03.11 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 23 선형 회귀분석 복습, 실습 (2) | 2025.03.10 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day22 머신러닝 기초, 로지스틱 회귀 실습 (0) | 2025.03.07 |



