1 통계의 정의와 목적
통계학이란?
통계학은 데이터를 수집, 정리, 분석, 해석하여 의미 있는 정보를 도출하는 학문입니다.
데이터를 통해 특정 현상의 패턴을 이해하고(특징), 이를 기반으로 예측하거나 의사 결정을 지원하는 데 활용됩니다.
현상 분석 → 기호로 바꿔야함(객관성 확보, 계산 가능) → 코드
통계 하는 이유: 기호로 만들기 위해선 통계뿐(수식이 있기에)
통계할때 범위가 중요함.
통계학은 크게 기술통계(Descriptive Statistics)와 추론통계(Inferential Statistics)로 구분.
1. 기술통계(Descriptive Statistics)
기술통계의 개념
기술통계는 데이터를 요약하고 정리하여 쉽게 이해할 수 있도록 표현하는 방법을 다룹니다. 주요 특징을 빠르게 파악할 수 있고, 비교와 분석이 용이.
- 모르는 데이터에서 특징을 잡아낼때 사용
- 산포도를 많이 씀
- 일반적으로는 컬럼을 알아야함
(1) 중심 경향 측정 (Central Tendency)
중심 경향 측정은 데이터의 중심 값을 찾는 방법으로, 대표적인 지표는 다음과 같습니다.
- 평균(Mean): 데이터가 정규분포를 따를 때 대표적인 값이 됩니다.
- 단점: 이상치(outlier)에 민감하여 왜곡될 가능성이 있음
- 중앙값(Median): 데이터를 크기순으로 정렬했을 때, 중앙에 위치하는 값입니다.
- 장점: 이상치의 영향을 받지 않음
- 단점: 데이터의 전체적인 특성을 나타내기에 부족할 수 있음
- 최빈값(Mode): 데이터에서 가장 자주 등장하는 값입니다.
- 장점: 범주형 데이터에서 유용하게 사용됨
- 단점: 데이터에 따라 최빈값이 없거나, 여러 개가 존재할 수 있음
(2) 산포도 측정 (Dispersion)
산포도는 데이터가 얼마나 흩어져 있는지를 나타내는 개념입니다. 데이터가 평균을 중심으로 얼마나 퍼져 있는지를 분석하는 것이 중요합니다.
- 범위(Range): 데이터의 최댓값과 최솟값의 차이를 의미합니다.
- 예시: 100(최댓값) - 60(최솟값) = 40
- 분산(Variance): 데이터 값들이 평균에서 얼마나 떨어져 있는지를 나타내는 지표입니다.
계산식:
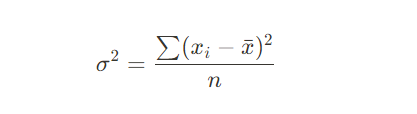
값이 클수록 데이터의 변동성이 크다는 것을 의미합니다.
→ 사용은 뭐 분산이 작아질때 구매를 하더라~ 이렇게 행동이랑 엮어서 활용할 수 있음.
- 표준편차(Standard Deviation): 분산의 제곱근을 구한 값으로, 데이터가 평균에서 얼마나 떨어져 있는지를 쉽게 해석할 수 있도록 변환한 값입니다
- 값이 클수록 데이터가 퍼져 있고, 작을수록 데이터가 평균에 가까운 값으로 모여 있음을 의미합니다.
- 계산식:
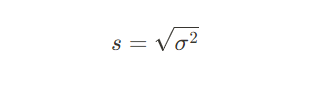
- 사분위 범위(Interquartile Range, IQR): 데이터의 1사분위(Q1)와 3사분위(Q3) 사이의 범위를 의미하며, 이상치를 판별하는 데 유용합니다.
- 이상치, anomaly 데이터에서 사용, 박스플롯에서도 정상 범주 잡을때 사용
계산식:
IQR = Q3 - Q1
#기술통계
import numpy as np
import pandas as pd
# 가상의 데이터 생성
data = [60, 70, 80, 80, 90, 100, 95, 85, 75, 65]
# 데이터프레임 생성
df = pd.DataFrame(data, columns=["점수"])
# 기술통계 요약
print(df.describe()) # 평균, 표준편차, 최솟값, 중앙값, 최댓값 등 출력
#출력값
점수
count 10.000000
mean 80.000000
std 12.909944
min 60.000000
25% 71.250000
50% 80.000000
75% 88.750000
max 100.000000
(3) 데이터 시각화
기술통계에서 데이터를 효과적으로 정리하고 해석하기 위해 다양한 시각화 기법을 활용할 수 있습니다.
- 히스토그램(Histogram): 데이터의 분포를 막대 그래프로 표현
- 박스플롯(Box Plot): 사분위수와 이상치를 한눈에 볼 수 있도록 정리
- 산점도(Scatter Plot): 두 변수 간의 관계를 나타내는 그래프
# 중심경향측정
mean_value = np.mean(data) # 평균
median_value = np.median(data) # 중앙값
mode_value = pd.Series(data).mode().values # 최빈값
print(f"평균: {mean_value}")
print(f"중앙값: {median_value}")
print(f"최빈값: {mode_value}")
#산포도측정
variance_value = np.var(data, ddof=1) # 분산 (모표본 사용)
std_dev_value = np.std(data, ddof=1) # 표준편차
range_value = np.max(data) - np.min(data) # 범위
iqr_value = np.percentile(data, 75) - np.percentile(data, 25) # 사분위 범위, IQR(사분위 범위) 계산 → 데이터의 중앙 50%가 차지하는 범위를 나타냄.
print(f"분산: {variance_value}")
print(f"표준편차: {std_dev_value}")
print(f"범위: {range_value}")
#IQR (Interquartile Range, 사분위 범위)는 데이터의 중앙 50%를 나타내는 범위로, 데이터 분포의 변동성을 측정하는 데 사용
print(f"사분위 범위: {iqr_value}")
#데이터 시각화
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(12, 5))
# 히스토그램
plt.subplot(1, 2, 1)
sns.histplot(data, bins=5, kde=True)
plt.title("히스토그램")
# 박스플롯
plt.subplot(1, 2, 2)
sns.boxplot(y=data)
plt.title("박스플롯")
plt.show()
평균: 80.0
중앙값: 80.0
최빈값: [80]
분산: 166.66666666666666
표준편차: 12.909944487358056
범위: 40
사분위 범위: 17.5

2. 추론통계(Inferential Statistics)
추론통계의 개념
추론통계는 표본(sample) 데이터를 이용하여 **모집단(population)**의 특성을 추정하는 방법입니다.
모든 데이터를 직접 수집하기 어려우므로 일부 데이터를 분석하여 전체를 예측하는 것이 핵심입니다.
추론통계의 주요 개념
추론통계에서는 가설검정, 신뢰구간, 회귀분석 등의 개념을 활용합니다.
(1) 가설검정(Hypothesis Testing)
가설검정은 주어진 데이터가 특정 가설을 뒷받침하는지 여부를 판단하는 과정입니다.
- 귀무가설(Null Hypothesis, H₀): "차이가 없다"는 기본 가설
- 대립가설(Alternative Hypothesis, H₁): "차이가 있다"는 가설
- 유의수준(Significance Level, α): 일반적으로 5%(0.05)를 사용.
- p < 0.05 → 귀무가설 기각 (유의미한 차이 있음)
- p ≥ 0.05 → 귀무가설 채택 (차이가 없음)
1.1 주요 가설검정 방법
검정 방법 목적 데이터 유형 사용 분포
| T-검정 (T-Test) | 두 집단의 평균 비교 | 연속형 데이터 (예: 점수, 체중) | T-분포 |
| 카이제곱 검정 (Chi-Square Test) | 범주형 변수 간 독립성 검정 | 범주형 데이터 (예: 성별, 지역) | 카이제곱 분포 |
| ANOVA(분산분석) | 세 집단 이상의 평균 비교 | 연속형 데이터 | F-분포 |
1.2 T-검정(T-Test)
✅ 두 집단의 평균 차이가 통계적으로 유의미한지 여부를 검정 비교
- 독립표본 T-검정: 서로 다른 두 집단 비교
- 대응표본 T-검정: 같은 집단의 전후 비교
T-검정 공식
독립표본 T-검정 (Independent T-Test)
두 독립적인 집단 $X_1$ 과 $X_2$ 의 평균 차이를 비교하는 공식:

- $\bar{X}_1,\bar{X}_2$
- : 두 집단의 샘플 평균
- $s_1^2,s_2^2$
- : 두 집단의 샘플 분산
- $n_1,n_2$
- : 두 집단의 샘플 크기
- 자유도 (Degrees of Freedom, df)
독립표본 T-검정에서 자유도는 보통 웰치의 자유도 공식(Welch-Satterthwaite equation) 을 사용하여 계산됩니다.

이 자유도를 사용하여 T-분포표에서 p-값을 계산합니다.
T-값을 이용하여 p-값을 계산하고, 보통 유의수준(α = 0.05)과 비교하여 결론을 내립니다.
- T검정 코드 예시
from scipy import stats # 라이브러리 임포트
# 두 집단 데이터 예시, 두개의 독립적인 그룹 정의
group1 = [80, 85, 88, 90, 95] # 첫 번째 집단 데이터
group2 = [70, 75, 78, 80, 85] # 두 번째 집단 데이터
# 독립표본 T-검정 (두 집단 평균 비교)
#stats.ttest_ind(group1, group2)`를 사용하여 독립표본 T-검정
#`t_stat`: T-검정 통계량 (두 그룹의 평균 차이를 표준오차로 나눈 값)
#`p_value`: P-값 (귀무가설이 참일 확률)
t_stat, p_value = stats.ttest_ind(group1, group2)
print(f"T-검정 통계량: {t_stat}")
print(f"P-값: {p_value}")
# **유의수준(α) = 0.05**을 기준으로 귀무가설 기각 여부 결정
if p_value < 0.05:
print("귀무가설 기각: 두 집단 간의 평균 차이가 통계적으로 유의미함")
else:
print("귀무가설 채택: 두 집단 간의 평균 차이가 없음")
#예상 출력 결과
T-검정 통계량: 3.162
P-값: 0.013
귀무가설 기각: 두 집단 간의 평균 차이가 통계적으로 유의미함
- T-검정을 사용할 때 주의할 점
- 정규성 검정(Normality Test) 필요
- T-검정은 데이터가 정규 분포를 따른다고 가정하므로, 데이터를 분석하기 전에 정규성 검정(Kolmogorov-Smirnov test, Shapiro-Wilk test 등)을 수행하는 것이 좋습니다.
- 등분산성 검정(Homogeneity of Variance) 필요
- 두 집단의 분산이 동일한지 확인해야 합니다. 분산이 다를 경우 웰치의 T-검정(Welch's T-Test)을 사용하는 것이 적절합니다.
- 샘플 크기 고려
- 샘플 크기가 작을 경우 정규성 가정을 위반할 수 있으므로 비모수 검정(예: Mann-Whitney U Test)을 고려할 수 있습니다.
- T-검정은 두 개의 독립적인 집단 간 평균 차이를 비교하는 통계적 방법입니다.
- P-값이 0.05보다 작으면 귀무가설을 기각하고, 평균 차이가 유의미하다고 판단합니다.
- 데이터가 정규성을 만족하는지 확인하는 것이 중요하며, 등분산 검정을 통해 분산이 동일한지도 평가해야 합니다.
- 정규성 검정(Normality Test) 필요
- T-검정을 사용할 때 주의할 점
1.3 카이제곱 검정(Chi-Square Test)
✅ 범주형 데이터 간 독립성 검정
- 예시: "광고 유형(A, B, C)에 따라 고객 유지율이 다른가?"
- 귀무가설(H₀): 광고 유형과 고객 유지율은 관계가 없다
- 대립가설(H₁): 광고 유형에 따라 고객 유지율이 다르다
- 카이제곱 검정 예제 코드
import numpy as np
import scipy.stats as stats
# 광고 유형별 고객 유지 여부 (예: 유지(Yes), 이탈(No))
# [유지, 이탈]
data = np.array([[200, 300], # 광고 A
[250, 250], # 광고 B
[150, 350]]) # 광고 C
# 카이제곱 검정 수행
chi2, p_value, _, _ = stats.chi2_contingency(data)
print(f"카이제곱 검정 통계량: {chi2}")
print(f"P-값: {p_value}")
if p_value < 0.05:
print("귀무가설 기각: 광고 유형에 따라 고객 유지율이 다름")
else:
print("귀무가설 채택: 광고 유형과 고객 유지율 간 유의미한 차이가 없음")
#출력값
카이제곱 검정 통계량: 41.66666666666667
P-값: 8.957736717696712e-10
귀무가설 기각: 광고 유형에 따라 고객 유지율이 다름
#광고 유형에 따른 고객 유지율 차이를 알아보기 위해 카이제곱 검정 수행.
#p값이 0.05보다 작기에 귀무가설 기각,
#광고유형에 따라 고객 유지율이 다르다고 볼 수 있음
#광고유형 효율성을 위해 추가 조사 필요
(2) 신뢰구간(Confidence Interval)
신뢰구간은 모집단의 평균을 포함할 가능성이 높은 값의 범위를 제공

예를 들어, 어떤 제품의 평균 수명이 50시간이고 표준편차가 5시간이며, 95% 신뢰구간을 구하면 특정 범위 내에서 평균값이 존재할 확률이 95%임을 의미합니다.
import scipy.stats as st
# 신뢰구간 95% 계산
confidence_level = 0.95
mean = np.mean(data)
std_error = stats.sem(data) # 표준오차
margin_of_error = std_error * st.t.ppf((1 + confidence_level) / 2, len(data) - 1)
lower_bound = mean - margin_of_error
upper_bound = mean + margin_of_error
print(f"95% 신뢰구간: ({lower_bound:.2f}, {upper_bound:.2f})")
(3) 회귀분석(Regression Analysis)
(Day 16에서 자세히 함)
회귀분석은 변수 간의 관계를 수학적으로 모델링하는 방법입니다.
- 단순 선형 회귀(Simple Linear Regression)
- 하나의 독립변수가 종속변수에 미치는 영향을 분석하는 모델
- 공식: 여기서 X는 독립변수, Y는 종속변수, a는 기울기, b는 절편을 의미

- 다중 선형 회귀(Multiple Linear Regression)
- 여러 개의 독립변수가 종속변수에 영향을 미치는 모델
- 공식:

import pandas as pd
from sklearn.linear_model import LinearRegression
# 모델 학습
X = df[["광고비"]]
y = df["매출"]
model = LinearRegression()
model.fit(X, y)
# 회귀 계수 출력
print(f"기울기(a): {model.coef_[0]}")
print(f"절편(b): {model.intercept_}")
# 예측
new_ad_cost = [[6000]]
predicted_sales = model.predict(new_ad_cost)
print(f"광고비 6000일 때 예상 매출: {predicted_sales[0]}")
2 데이터 분포와 확률
데이터 분석과 확률 이론에서 **데이터 분포(Data Distribution)와 확률(Probability)**는 매우 중요한 개념입니다. 이를 이해하면 데이터의 특성을 파악하고, 예측 모델을 구축하는 데 도움을 줄 수 있습니다.
1. 데이터 분포 (Data Distribution)
데이터 분포는 데이터를 시각적으로 표현하고 분석하는 데 사용됩니다. 데이터가 어떻게 분포되어 있는지에 따라 분석 방법과 적용 모델이 달라질 수 있습니다.
1.1 데이터 분포의 유형
(1) 정규 분포 (Normal Distribution)
- 종 모양(Bell Curve)을 가진 대칭적인 분포
- 평균(μ)과 표준편차(σ)로 정의됨
- 자연현상과 많은 데이터셋에서 흔히 나타남 (예: 키, 시험 점수, 혈압 등)
- 중심극한정리(Central Limit Theorem)에 의해 많은 확률변수가 정규 분포를 따름
(2) 균등 분포 (Uniform Distribution)
- 모든 값이 동일한 확률을 가짐
- 예: 주사위를 던질 때 각 면이 나올 확률이 동일함 (1/6)
(3) 이항 분포 (Binomial Distribution)
- 특정 사건이 여러 번 반복될 때, 성공과 실패의 횟수를 따지는 분포
- 예: 동전을 10번 던졌을 때 앞면이 나오는 횟수
(4) 포아송 분포 (Poisson Distribution)
- 일정 시간이나 공간 내에서 발생하는 사건의 횟수를 모델링하는 데 사용
- 예: 고객이 1시간 동안 매장에 방문하는 횟수
(5) 지수 분포 (Exponential Distribution)
- 사건이 발생하는 시간 간격을 모델링
- 예: 고객이 매장에 도착하는 시간 간격
(6) 감마 분포 (Gamma Distribution)
- 지수 분포를 일반화한 분포로, 연속적인 시간 간격을 모델링할 때 사용
(7) 카이제곱 분포 (Chi-Square Distribution)
- 정규 분포를 따르는 여러 변수들의 제곱합을 따르는 분포
- 예: 분산 분석(ANOVA)에서 사용됨
(8) 정규성 검정 (Normality Test)
- 데이터가 정규 분포를 따르는지 확인하는 방법
- Kolmogorov-Smirnov test, Shapiro-Wilk test 등이 있음
2. 확률 (Probability)
확률은 특정 사건이 발생할 가능성을 수학적으로 나타낸 값입니다. 확률값은 0에서 1 사이의 값을 가지며, 1에 가까울수록 해당 사건이 발생할 가능성이 높음을 의미합니다.
2.1 확률의 기본 개념
- 확률(P): 사건이 일어날 가능성 (0 ≤ P(A) ≤ 1)
- 표본 공간(Sample Space, S): 가능한 모든 경우의 집합
- 사건(Event, E): 관심 있는 결과들의 집합
2.2 확률 계산법
(1) 고전적 확률 (Classical Probability)
- 모든 경우가 동일한 확률을 가질 때 사용
- 예: 동전을 던질 때 앞면이 나올 확률 = 1/2
(2) 경험적 확률 (Empirical Probability)
- 실제 데이터를 기반으로 계산
- 예: 과거 데이터를 통해 비 오는 날의 확률을 추정
(3) 조건부 확률 (Conditional Probability)
- 특정 사건이 발생했을 때 다른 사건이 발생할 확률
- 예: 어떤 사람이 감기에 걸렸을 때, 병원을 방문할 확률
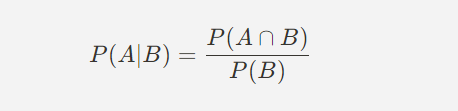
(4) 독립 사건과 종속 사건
- 독립 사건(Independent Event): 한 사건의 발생이 다른 사건에 영향을 주지 않음 (예: 주사위를 두 번 던지는 경우)
- 종속 사건(Dependent Event): 한 사건이 발생하면 다른 사건의 확률이 바뀜 (예: 카드를 한 장 뽑은 후 다시 섞지 않고 두 번째 카드를 뽑는 경우)
(5) 베이즈 정리 (Bayes' Theorem)
- 사전 확률(Prior Probability)과 새로운 증거를 이용해 사후 확률(Posterior Probability)을 계산하는 공식
- 예: 의료 진단에서 특정 질병이 있을 확률을 예측할 때 사용

데이터의 종류와 특성 정리표
| 구분 | 설명 | 예시 | 분류 | 특징 |
| 정성 데이터 (Qualitative Data) | 숫자로 표현되지 않는 데이터 (범주형 데이터) | 성별(남/여), 혈액형(A/B/O/AB), 지역(서울/부산/대구) | 명목형 데이터 (Nominal Data) | 순서 없음 (예: 혈액형, 성별) |
| 서열형 데이터 (Ordinal Data) | 순서 있음 (예: 만족도 설문 - "불만족" → "보통" → "만족") | |||
| 정량 데이터 (Quantitative Data) | 숫자로 표현되며 연산이 가능한 데이터 | 키(170cm), 체중(70kg), 시험 점수(90점) | 이산형 데이터 (Discrete Data) | 특정 값만 가능 (예: 학생 수, 자동차 개수) |
| 연속형 데이터 (Continuous Data) | 특정 구간 내에서 무한한 값 가능 (예: 온도, 키, 몸무게) |
회고
오늘은 확률 overview라서 개념 훑고, 제시된 코드로 돌려보는걸 했다.
데이터 분포별 특징, 가설검정 예시 보고 싶으면 GM15 코드 참고할 것.
뒤에서 추가적으로 배우는 내용있으면 수정할 것.
'STUDY' 카테고리의 다른 글
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day17 상관관계, 회귀, 상관분석 보고서 실습 (0) | 2025.03.07 |
|---|---|
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day16 회귀분석, 보고서 실습 (0) | 2025.03.07 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 14 EDA, EDA 데이터 전처리 종합 실습 (0) | 2025.03.05 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 13-2 데이터 표준화, 정규화 (0) | 2025.02.26 |
| [멋쟁이사자처럼부트캠프_그로스마케팅] Day 13-1 이상치, 데이터 변환(결측치, 데이터 타입 변환) (0) | 2025.02.26 |



